Find the System of Equations to Model the Problem

Essay

Find the system of equations to model the problem. DO NOT SOLVE THIS SYSTEM.
-A paper company produces high, medium, and low grade paper. The number of tons of each grade that is produced
from one ton of pulp depends on the source of that pulp. The following table lists three sources and the amount of each
grade of paper that can be made for one ton of pulp from each source. 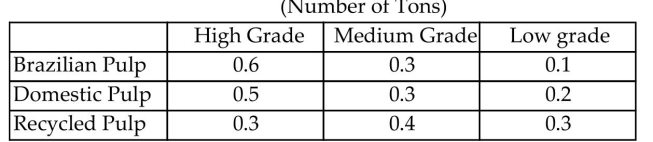The paper company has orders for 11 tons of high grade, 15 tons of medium grade, and 14 tons of low grade paper.
How many tons of each type of pulp should be used to fill these orders exactly? Set up a system of linear equations,
letting x, y, and z be the number of tons of Brazilian pulp, domestic pulp, and recycled pulp, respectively, needed to fill
the orders.