Solved

Solve the Problem. -The Expected Future Population of a Small Town, Which Currently

Question 135

Multiple Choice

Solve the problem.
-The expected future population of a small town, which currently has 7900 residents, can be approximated by the formula Solve the problem. -The expected future population of a small town, which currently has 7900 residents, can be approximated by the formula 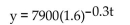where t is the number of years in the future. Find the expected population of the town 50 years in the future. A) 0 B) 3792 C) 7900 D) 7 where t is the number of years in the future. Find the expected population of the town 50 years in the future.


A) 0
B) 3792
C) 7900
D) 7

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q130: Evaluate.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8475/.jpg" alt="Evaluate. - A) 15

Q131: Solve the problem.<br>-The value V of a

Q132: Approximate the following value. Round to four

Q133: Solve the problem.<br>-Find out how long it

Q134: Approximate the following value. Round to four

Q136: Evaluate.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8475/.jpg" alt="Evaluate. - A) 4.8

Q137: For the given functions f and g

Q138: Determine whether the function is a one-to-one

Q139: For the given functions f and g

Q140: Determine whether the function is a one-to-one