Solved

Use the Definition of a Logarithm to Find an Equivalent

Question 71

Multiple Choice

Use the definition of a logarithm to find an equivalent equation.
-

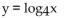
A) Use the definition of a logarithm to find an equivalent equation. - A) 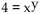B) 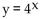C) 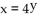D)
B)
C)
D)

Related Questions

Q66: Determine whether the given functions are inverses

Q67: The following equation is in the form

Q68: Use properties of logarithms to expand the

Q69: Evaluate.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8475/.jpg" alt="Evaluate. - A) 7

Q70: Solve the problem.<br>-How many times more intense

Q72: Find the unknown value.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8475/.jpg" alt="Find the

Q73: Determine whether the given functions are inverses

Q74: Use the change of base formula to

Q75: Find the power of 10. Round answers

Q76: Write the equation in exponential form.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8475/.jpg"