Solved

X Is a Continuous Random Variable with Mean µ and Standard

Question 16

Multiple Choice

X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ)
if
-X is an exponential random variable with m = 2 ln 2.


A) X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if -X is an exponential random variable with m = 2 ln 2. A) B) C) D)
B) X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if -X is an exponential random variable with m = 2 ln 2. A) B) C) D)
C) X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if -X is an exponential random variable with m = 2 ln 2. A) B) C) D)
D) X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if -X is an exponential random variable with m = 2 ln 2. A) 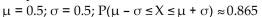B) 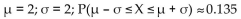C) 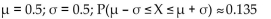D)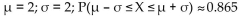

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q11: X is a continuous random variable with

Q12: Use a graphing calculator to approximate the

Q13: Solve the problem.<br>-When a person takes a

Q14: Solve the problem.<br>-A building contractor's profit (in

Q15: Given a normal distribution with mean 150

Q17: Solve the problem.<br>-The life expectancy of a

Q18: Find the associated cumulative distribution function. Graph

Q19: Find the value of the improper integral

Q20: Solve the problem.<br>-A trust fund produces a

Q21: Given a normal distribution with mean 40