Solved

A Common Inhabitant of Human Intestines Is the Bacterium

Question 58

Multiple Choice

A common inhabitant of human intestines is the bacterium 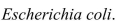A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E) A cell of this bacterium in a nutrient-broth medium divides into two cells every A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E) The initial population of a culture is A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E) cells.Find the number of cells after A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E) hours.


A) A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E)
B) A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E)
C) A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E)
D) A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is cells.Find the number of cells after hours. A) B) C) D) E)
E) A common inhabitant of human intestines is the bacterium A cell of this bacterium in a nutrient-broth medium divides into two cells every The initial population of a culture is 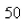cells.Find the number of cells after 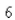hours. A) 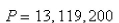B) 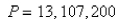C) D) 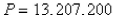E)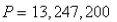

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q53: Choose the differential equation corresponding to this

Q54: Select the correct Answer: for each question.<br>-Suppose

Q55: Solve the initial-value problem. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Solve

Q56: Let c be a positive number.A differential

Q57: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Solve

Q59: Consider a population <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Consider a

Q60: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Solve

Q61: Find the orthogonal trajectories of the family

Q62: A sum of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="A sum

Q63: Choose the differential equation corresponding to this