Essay
A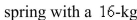 
mass has natural length 
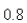m and is maintained stretched to a length of 
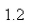m by a force of 
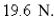If the spring is compressed to a length of 
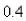m and then released with zero velocity, find the position 
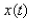of the mass at any time .
Correct Answer:
Verified
Correct Answer:
Verified
Related Questions
Q5: Solve the differential equation using the method
Q6: A spring with a mass of 2
Q7: Suppose a spring has mass M and
Q8: Solve the differential equation using the method
Q9: The solution of the initial-value problem <img
Q11: Solve the boundary-value problem, if possible. <img
Q12: Graph the particular solution and several other
Q13: Suppose a spring has mass M and
Q14: Solve the differential equation using the method
Q15: Solve the differential equation using the method