Solved

Find the Area of the Part of the Sphere

Question 63

Multiple Choice

Find the area of the part of the sphere Find the area of the part of the sphere that lies inside the paraboloid Select the correct Answer A) B) C) D) E) that lies inside the paraboloid Find the area of the part of the sphere that lies inside the paraboloid Select the correct Answer A) B) C) D) E) Select the correct Answer


A) Find the area of the part of the sphere that lies inside the paraboloid Select the correct Answer A) B) C) D) E)
B) Find the area of the part of the sphere that lies inside the paraboloid Select the correct Answer A) B) C) D) E)
C) Find the area of the part of the sphere that lies inside the paraboloid Select the correct Answer A) B) C) D) E)
D) Find the area of the part of the sphere that lies inside the paraboloid Select the correct Answer A) B) C) D) E)
E) Find the area of the part of the sphere 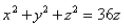that lies inside the paraboloid 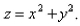Select the correct Answer A) 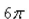B) 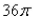C) 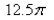D) E)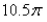

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q58: Find the volume of the solid bounded

Q59: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Evaluate and

Q60: Select the correct Answer for each question.<br>-Use

Q61: Select the correct Answer for each question.<br>-Use

Q62: Select the correct Answer for each question.<br>-Use

Q64: Select the correct Answer for each question.<br>-Evaluate

Q65: Calculate the iterated integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Calculate

Q66: Use a computer algebra system to find

Q67: Use a double integral to find the

Q68: Use cylindrical coordinates to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg"