Solved

Use the Alternating Series Estimation Theorem or Taylor's Inequality to Estimate

Question 7

Essay

Use the Alternating Series Estimation Theorem or Taylor's Inequality to estimate the range of values of x for which the given approximation is accurate to within the stated error. Use the Alternating Series Estimation Theorem or Taylor's Inequality to estimate the range of values of x for which the given approximation is accurate to within the stated error. Write a such that Write a such that Use the Alternating Series Estimation Theorem or Taylor's Inequality to estimate the range of values of x for which the given approximation is accurate to within the stated error. 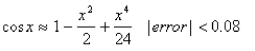Write a such that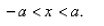

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q2: Select the correct Answer for each question.<br>-If

Q3: Determine whether the geometric series converges or

Q4: Find the interval of convergence of the

Q5: Express the numb <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg" alt="Express the

Q6: Determine whether the given series converges or

Q8: Find a power series representation for the

Q9: Determine whether the given series converges or

Q10: Use the power series for <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8680/.jpg"

Q11: Select the correct Answer for each question.<br>-Test

Q12: Test the series for convergence or divergence.