Solved

Use an Iterated Integral to Find the Area of the Region

Question 29

Multiple Choice

Use an iterated integral to find the area of the region bounded by the graphs of the equations Use an iterated integral to find the area of the region bounded by the graphs of the equations A) B) C) D) E)


A) Use an iterated integral to find the area of the region bounded by the graphs of the equations A) B) C) D) E)
B) Use an iterated integral to find the area of the region bounded by the graphs of the equations A) B) C) D) E)
C) Use an iterated integral to find the area of the region bounded by the graphs of the equations A) B) C) D) E)
D) Use an iterated integral to find the area of the region bounded by the graphs of the equations A) B) C) D) E)
E) Use an iterated integral to find the area of the region bounded by the graphs of the equations 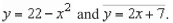A) 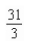B) 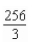C) D) E)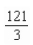

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q24: Evaluate the following iterated integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8202/.jpg"

Q25: Evaluate the iterated integral below.Note that it

Q26: Evaluate the following iterated integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8202/.jpg"

Q27: Evaluate the following improper integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8202/.jpg"

Q28: Use a double integral to find the

Q30: Evaluate the following iterated integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8202/.jpg"

Q31: Evaluate the iterated integral below.Note that it

Q32: Use an iterated integral to find the

Q33: Set up and evaluate a double integral

Q34: Use an iterated integral to find the