Multiple Choice
Solve.
-A ball is dropped from a height of 25 feet. Each time it strikes the ground, it bounces up to 0.7 of theprevious height. The total distance the ball has traveled before the second bounce is 25 + 2(25 ∙ 0.7) feet,and the total distance the ball has traveled before bounce n + 1 is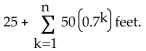 
Use facts about infinite geometric series to calculate the total distance the ball has traveled by the time it hasstopped bouncing.
A) 
B)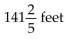 
C)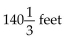 
D)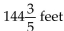 
Correct Answer:
Verified
Correct Answer:
Verified
Q138: Write out the first five terms of
Q139: Find the indicated term using the given
Q140: Determine whether the sequence is arithmetic.<br>-2, 4,
Q141: Find the sum of the sequence.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8253/.jpg"
Q142: Determine whether the given sequence is arithmetic,
Q144: Use the Binomial Theorem to find the
Q145: Use the Binomial Theorem to find the
Q146: Expand the expression using the Binomial Theorem.<br>-<img
Q147: Find the sum.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8253/.jpg" alt="Find the sum.
Q148: A geometric sequence is given. Find the