Solved

Decide Whether or Not the Functions Are Inverses of Each

Question 39

Multiple Choice

Decide whether or not the functions are inverses of each other.
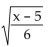
-f(x) = Decide whether or not the functions are inverses of each other. -f(x) = g(x) = A) Yes; Exclude the interval (-∞, 5) B) Yes; No values need to be excluded. C) Yes; Exclude the interval (-∞, 6) D) No g(x) = Decide whether or not the functions are inverses of each other. -f(x) = g(x) = A) Yes; Exclude the interval (-∞, 5) B) Yes; No values need to be excluded. C) Yes; Exclude the interval (-∞, 6) D) No


A) Yes; Exclude the interval (-∞, 5)
B) Yes; No values need to be excluded.
C) Yes; Exclude the interval (-∞, 6)
D) No

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q34: Find the inverse function of f. State

Q35: Solve the problem.<br>-The number of books in

Q36: Solve the equation.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8253/.jpg" alt="Solve the equation.

Q37: Approximate the value using a calculator. Express

Q38: Use the horizontal line test to determine

Q40: Solve the problem.<br>-Hector borrows $2,500 at a

Q41: Approximate the value using a calculator. Express

Q42: The function f is one-to-one. Find its

Q43: For the given functions f and g,

Q44: Decide whether the composite functions, f ∘