Solved

Change the Logarithmic Expression to an Equivalent Expression Involving an Exponent

Question 15

Multiple Choice

Change the logarithmic expression to an equivalent expression involving an exponent.
-Change the logarithmic expression to an equivalent expression involving an exponent. - A) B) C) D)


A) Change the logarithmic expression to an equivalent expression involving an exponent. - A) B) C) D)
B) Change the logarithmic expression to an equivalent expression involving an exponent. - A) B) C) D)
C) Change the logarithmic expression to an equivalent expression involving an exponent. - A) B) C) D)
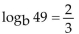
D) Change the logarithmic expression to an equivalent expression involving an exponent. - A) 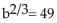B) 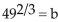C) 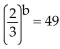D)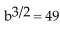

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q10: Indicate whether the function is one-to-one.<br>-{(-5, -9),

Q11: Find the domain of the composite function

Q12: Use the graph of the given one-to-one

Q13: Solve the problem.<br>-Find a so that the

Q14: Find the exact value of the logarithmic

Q16: Find the domain of the composite function

Q17: Solve the equation.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8253/.jpg" alt="Solve the equation.

Q18: The graph of a one-to-one function f

Q19: Find a formula for the inverse of

Q20: Change the logarithmic expression to an equivalent