Solved

Form a Polynomial Whose Zeros and Degree Are Given

Question 26

Multiple Choice

Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1.
-Zeros: 2, multiplicity 2; -2, multiplicity 2; degree 4


A) Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1. -Zeros: 2, multiplicity 2; -2, multiplicity 2; degree 4 A) B) C) D)
B) Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1. -Zeros: 2, multiplicity 2; -2, multiplicity 2; degree 4 A) B) C) D)
C) Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1. -Zeros: 2, multiplicity 2; -2, multiplicity 2; degree 4 A) B) C) D)
D) Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1. -Zeros: 2, multiplicity 2; -2, multiplicity 2; degree 4 A) 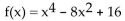B) 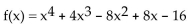C) 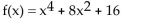D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q21: For the polynomial, list each real zero

Q22: State whether the function is a polynomial

Q23: For the polynomial, list each real zero

Q24: Use transformations of the graph of <img

Q25: Use transformations of the graph of <img

Q27: Form a polynomial whose zeros and degree

Q28: State whether the function is a polynomial

Q29: Use transformations of the graph of <img

Q30: For the polynomial, list each real zero

Q31: State whether the function is a polynomial