SCENARIO 15-4 the Superintendent of a School District Wanted to Predict

Multiple Choice

SCENARIO 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) , daily mean of the percentage of students attending class (% Attendance) , mean teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, 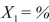Attendance, 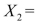Salaries and Spending. The coefficient of multiple determination ( 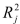) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: 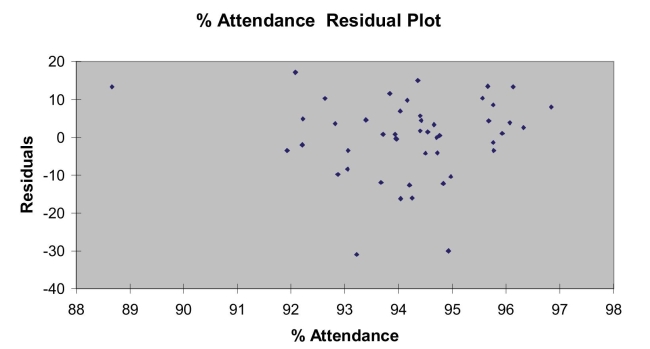Following is the output of several multiple regression models: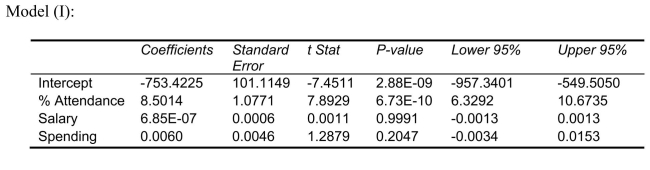
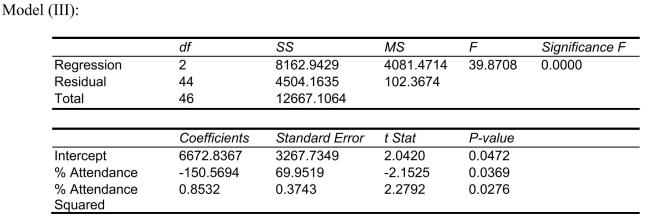
-Referring to Scenario 15-4, the "best" model chosen using the adjusted R-square statistic is

A)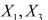
B)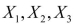
C) either of the above
D) None of the above