Multiple Choice
SCENARIO 18-6 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) .Two variables thought to affect weight-loss are client's length of time on the weight loss program and time of session.These variables are described below: Y = Weight-loss (in pounds) 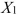 = Length of time in weight-loss program (in months)
= Length of time in weight-loss program (in months) 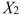 = 1 if morning session, 0 if not
= 1 if morning session, 0 if not 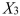 = 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
= 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: 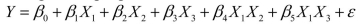 Partial output from Microsoft Excel follows:
Partial output from Microsoft Excel follows: 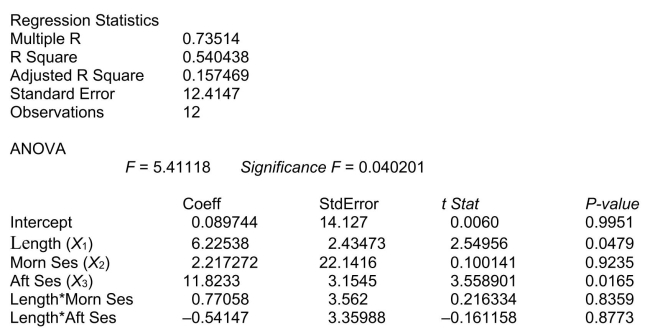
-Referring to Scenario 18-6, what null hypothesis would you test to determine whether the slope of the linear relationship between weight-loss (Y) and time in the program (x₁) varies according to time of session?
A) 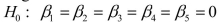
B) 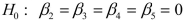
C) 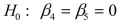
D) 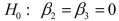
Correct Answer:

Verified
Correct Answer:
Verified
Q8: SCENARIO 18-12<br>The marketing manager for a nationally
Q121: SCENARIO 18-9<br>What are the factors that determine
Q208: SCENARIO 18-11 A logistic regression model was
Q209: SCENARIO 18-9 What are the factors that
Q210: SCENARIO 18-10 Given below are results from
Q217: SCENARIO 18-10 Given below are results from
Q218: SCENARIO 18-10 Given below are results from
Q226: SCENARIO 18-9<br>What are the factors that determine
Q258: SCENARIO 18-12<br>The marketing manager for a nationally
Q300: SCENARIO 18-12<br>The marketing manager for a nationally