Solve the Problem. -The Population of One Town Is Modeled by the Function

Multiple Choice

Solve the problem.
-The population of one town is modeled by the function P(t) = 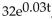and the population of a second town is modeled by the function P(t) = 32 + 1.2t. In each case, t is the number of years from the present, and P(t) is given
In thousands of people. In how many years is the population of the first town predicted to be twice as large as
The population of the second town? (Round to the nearest tenth of a year.)

A) 63.8 years
B) 16.2 years
C) 61.7 years
D) 24.7 years