Solved

Use Odd and Even Identities to Simplify the Expression

Question 588

Multiple Choice

Use odd and even identities to simplify the expression.
-(1 + csc x) (1 + csc(-x) )


A) Use odd and even identities to simplify the expression. -(1 + csc x) (1 + csc(-x) ) A) B) C) D)
B) Use odd and even identities to simplify the expression. -(1 + csc x) (1 + csc(-x) ) A) B) C) D)
C) Use odd and even identities to simplify the expression. -(1 + csc x) (1 + csc(-x) ) A) B) C) D)
D) Use odd and even identities to simplify the expression. -(1 + csc x) (1 + csc(-x) ) A) B) 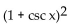C) 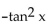D)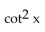

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q583: Solve the problem.<br>-The weekly sales in thousands

Q584: Determine whether the positive or negative sign

Q585: Use a sum or difference identity to

Q586: Multiply and simplify.<br>-(1 - sec <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8458/.jpg"

Q587: Find the product.<br>-(2 sin y - 3)(sin

Q589: Prove that the equation is an identity.<br>-<img

Q590: Prove the identity.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8458/.jpg" alt="Prove the identity.

Q591: Find all angles in degrees that satisfy

Q592: Write in terms of the cofunction of

Q593: Use identities to simplify the expression.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8458/.jpg"