Solved

Use the Rational Zero Theorem to Find All Possible Rational

Question 349

Multiple Choice

Use the rational zero theorem to find all possible rational zeros for the polynomial function.
-P(x) = Use the rational zero theorem to find all possible rational zeros for the polynomial function. -P(x) = + 9x - 8 A) B) C) D) + 9x - 8


A) Use the rational zero theorem to find all possible rational zeros for the polynomial function. -P(x) = + 9x - 8 A) B) C) D)
B) Use the rational zero theorem to find all possible rational zeros for the polynomial function. -P(x) = + 9x - 8 A) B) C) D)
C) Use the rational zero theorem to find all possible rational zeros for the polynomial function. -P(x) = + 9x - 8 A) B) C) D)
D) Use the rational zero theorem to find all possible rational zeros for the polynomial function. -P(x) = + 9x - 8 A) B) 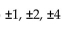C) 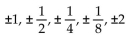D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q344: Solve the problem.<br>-The polynomial function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8458/.jpg"

Q345: Find the product.<br>-(x - 3i)(x + 3i)<br>A)

Q346: Provide an appropriate response.<br>-Is it possible to

Q347: Describe the behavior of the function's graph

Q348: Identify the solution set to the inequality

Q350: Use the factor theorem to decide whether

Q351: Find all real and imaginary solutions.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8458/.jpg"

Q352: Solve the polynomial inequality. State the solution

Q353: Find the product.<br>-[x - (2 + 4i)][x

Q354: Solve the absolute value equation.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8458/.jpg" alt="Solve