Solved

Write a Formula for the Nth Term of the Given

Question 329

Multiple Choice

Write a formula for the nth term of the given geometric sequence. Do not use a recursion formula.
-Write a formula for the nth term of the given geometric sequence. Do not use a recursion formula. - A) B) C) D)


A) Write a formula for the nth term of the given geometric sequence. Do not use a recursion formula. - A) B) C) D)
B) Write a formula for the nth term of the given geometric sequence. Do not use a recursion formula. - A) B) C) D)
C) Write a formula for the nth term of the given geometric sequence. Do not use a recursion formula. - A) B) C) D)
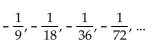
D) Write a formula for the nth term of the given geometric sequence. Do not use a recursion formula. - A) 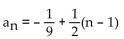B) C) D)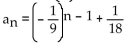

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q324: Solve the problem.<br>-A sports shop sold tennis

Q325: Determine whether the statement is true for

Q326: Find the probability of the event.<br>-If a

Q327: Solve the problem.<br>-How many distinct triangles are

Q328: Write the series in summation notation. Use

Q330: Write the first four terms of the

Q331: Find the indicated part of the arithmetic

Q332: Provide an appropriate response.<br>-Consider the possible selections

Q333: Solve the problem.<br>-A town has a population

Q334: Write the first four terms of the