Solved

Determine Whether the Given Function Is One-To-One

Question 218

Multiple Choice

Determine whether the given function is one-to-one. If so, find a formula for the inverse.
-f(x) = 4x + 3


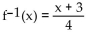
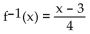
A) Determine whether the given function is one-to-one. If so, find a formula for the inverse. -f(x) = 4x + 3 A) B) C) D) Not a one-to-one function
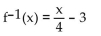
B) Determine whether the given function is one-to-one. If so, find a formula for the inverse. -f(x) = 4x + 3 A) B) C) D) Not a one-to-one function
C) Determine whether the given function is one-to-one. If so, find a formula for the inverse. -f(x) = 4x + 3 A) B) C) D) Not a one-to-one function
D) Not a one-to-one function

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q213: Find the logarithm.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8504/.jpg" alt="Find the logarithm.

Q214: Solve the problem. When appropriate, round the

Q215: Find the requested composition of functions.<br>-Given f(x)

Q216: Solve the equation.<br>-log ( 5 + x)

Q217: Solve the equation.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8504/.jpg" alt="Solve the equation.

Q219: Solve the problem.<br>-Use the formula <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8504/.jpg"

Q220: Express as a single logarithm.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8504/.jpg" alt="Express

Q221: Solve.<br>-Given <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8504/.jpg" alt="Solve. -Given

Q222: Solve the equation.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8504/.jpg" alt="Solve the equation.

Q223: Use a calculator and the change-of-base formula