Solved

Life Expectancy an Actuary Wanted to Develop a Model to Predict

Question 17

Essay

Life Expectancy An actuary wanted to develop a model to predict how long individuals will live. After consulting a number of physicians, she collected the age at death ( y ), the average number of hours of exercise per week ( x 1), the cholesterol level ( x 2), and the number of points that the individual's blood pressure exceeded the recommended value ( x 3). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79 x 1 - 0.021 x 2 - 0.061 x 3 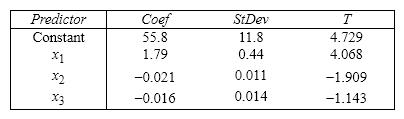Life Expectancy An actuary wanted to develop a model to predict how long individuals will live. After consulting a number of physicians, she collected the age at death ( y ), the average number of hours of exercise per week ( x <sub>1</sub>), the cholesterol level ( x <sub>2</sub>), and the number of points that the individual's blood pressure exceeded the recommended value ( x <sub>3</sub>). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79 x <sub>1</sub> - 0.021 x <sub>2</sub> - 0.061 x <sub>3</sub> S = 9.47 R - Sq = 22.5% ANALYSIS OF VARIANCE {Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the model is useful in predicting length of life?

S = 9.47 R - Sq = 22.5%
ANALYSIS OF VARIANCE Life Expectancy An actuary wanted to develop a model to predict how long individuals will live. After consulting a number of physicians, she collected the age at death ( y ), the average number of hours of exercise per week ( x <sub>1</sub>), the cholesterol level ( x <sub>2</sub>), and the number of points that the individual's blood pressure exceeded the recommended value ( x <sub>3</sub>). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79 x <sub>1</sub> - 0.021 x <sub>2</sub> - 0.061 x <sub>3</sub> S = 9.47 R - Sq = 22.5% ANALYSIS OF VARIANCE {Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the model is useful in predicting length of life? {Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the model is useful in predicting length of life?

Correct Answer:

verifed

Verified

blured image blured image At least one b i is not equal to zero. ...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q13: Life Expectancy An actuary wanted to develop

Q14: Real Estate Builder A real estate builder

Q15: Marc Anthony Concert At a recent Marc

Q22: Student's Final Grade A statistics professor investigated

Q33: We test an individual coefficient in a

Q43: One of the consequences of multicollinearity in

Q96: How do you go about checking for

Q129: Multicollinearity is present if the dependent variable

Q140: Some of the requirements for the error

Q170: When the error variable does not have