Solved

DeMoivre's Theorem Can Be Used to Find Reciprocals of Complex

Question 85

Essay

DeMoivre's Theorem can be used to find reciprocals of complex numbers. Recall from algebra that the reciprocal of x is DeMoivre's Theorem can be used to find reciprocals of complex numbers. Recall from algebra that the reciprocal of x is , which can be expressed as Use this fact, along with DeMoivre's Theorem, to find the reciprocal of the number below. , which can be expressed as DeMoivre's Theorem can be used to find reciprocals of complex numbers. Recall from algebra that the reciprocal of x is , which can be expressed as Use this fact, along with DeMoivre's Theorem, to find the reciprocal of the number below. Use this fact, along with DeMoivre's Theorem, to find the reciprocal of the number below. DeMoivre's Theorem can be used to find reciprocals of complex numbers. Recall from algebra that the reciprocal of x is 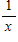, which can be expressed as 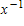Use this fact, along with DeMoivre's Theorem, to find the reciprocal of the number below.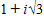

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q80: Change the equation to rectangular coordinates and

Q81: Graph the ordered pair on a polar

Q82: Find 4 fourth roots of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX9354/.jpg"

Q83: Find two square roots for the complex

Q84: Find three cube roots for the complex

Q86: Find the product. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX9354/.jpg" alt="Find the

Q87: If z is a complex number, show

Q88: Write the complex number in trigonometric form.

Q89: Write the complex number in standard form.

Q90: Multiply. Leave the answer in trigonometric form.