Solved

In Order to Justify the Construction of the Angle-Bisector

Question 65

Multiple Choice

In order to justify the construction of the angle-bisector 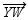In order to justify the construction of the angle-bisector of , we verify that two triangles are congruent by which method? A) SAS B) ASA C) SSS D) HL of In order to justify the construction of the angle-bisector of , we verify that two triangles are congruent by which method? A) SAS B) ASA C) SSS D) HL , we verify that two triangles are congruent by which method?


A) SAS
B) ASA
C) SSS
D) HL

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q61: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="Given that

Q62: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="Given that

Q63: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="If in

Q64: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="Given that

Q66: Given that point P is the midpoint

Q67: In the figure, <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="In the

Q68: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="Given that

Q159: In a right triangle, the length of

Q694: In the construction a regular hexagon, we

Q837: The reason for the congruence of two