Externally Tangent Circles P and Q Touch at Point T

Question 19

Not Answered

Externally tangent circles P and Q touch at point T and have the line of centers Externally tangent circles P and Q touch at point T and have the line of centers 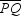. How does one construct the common internal tangent for circles P and Q ? . How does one construct the common internal tangent for circles P and Q ?

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q14: If m <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="If m

Q15: In the circle, m <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="In

Q16: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt=" is tangent to

Q17: In the figure, suppose that auxiliary line

Q20: In the figure, secants <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="In

Q21: In <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="In ,

Q23: In the figure, chords <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="In

Q447: When two secants intersect at a point

Q625: Two circles that are internally tangent have

Q877: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -The circles shown