Solved

Find the Point of Intersection for the Lines Whose Equations

Question 18

Multiple Choice

Find the point of intersection for the lines whose equations are 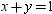Find the point of intersection for the lines whose equations are and . A) B) C) D) and Find the point of intersection for the lines whose equations are and . A) B) C) D) .


A) Find the point of intersection for the lines whose equations are and . A) B) C) D)
B) Find the point of intersection for the lines whose equations are and . A) B) C) D)
C) Find the point of intersection for the lines whose equations are and . A) B) C) D)
D) Find the point of intersection for the lines whose equations are and 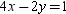. A) B) 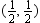C) D)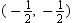

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q13: Where <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="Where ,

Q14: Let the vertices of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="Let

Q17: In the form <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="In the

Q20: What is the value of x at

Q21: The fourth vertex of the parallelogram shown

Q23: Given that A = (-3,-7)and B =

Q104: While the coordinate axes separate the Cartesian

Q264: The triangle with vertices at (0, 0),

Q469: Points A and B have symmetry with

Q890: If the diagonals of a parallelogram are