Solved

In the Form , Find the Equation of the Line

Question 51

Multiple Choice

In the form In the form , find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2 a ,2 b ) . A) B) C) D) , find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2 a ,2 b ) .


A) In the form , find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2 a ,2 b ) . A) B) C) D)
B) In the form , find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2 a ,2 b ) . A) B) C) D)
C) In the form , find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2 a ,2 b ) . A) B) C) D)
D) In the form , find the equation of the line that is the perpendicular- bisector of the line segment that joins (0,0) and (2 a ,2 b ) . A) 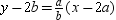B) 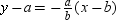C) 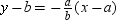D)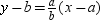

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q48: The line through the points ( a

Q50: The point <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8811/.jpg" alt="The point

Q52: According to the Midpoint Formula, the midpoint

Q53: If midpoints are involved in a proof,

Q54: Find the y-coordinate of point X =

Q55: Find the point of intersection for the

Q56: Determine the exact volume of the sphere

Q120: In Cartesian space, the point (0,6,0) lies

Q805: What type of triangle has vertices at

Q911: To show analytically that two lines are