Solved

For the Differential Equation, Find the Particular Solution Y =

Question 57

Multiple Choice

For the differential equation, find the particular solution y = 0 when x = 0. For the differential equation, find the particular solution y = 0 when x = 0. A) B) C) D) E)


A) For the differential equation, find the particular solution y = 0 when x = 0. A) B) C) D) E)
B) For the differential equation, find the particular solution y = 0 when x = 0. A) B) C) D) E)
C) For the differential equation, find the particular solution y = 0 when x = 0. A) B) C) D) E)
D) For the differential equation, find the particular solution y = 0 when x = 0. A) B) C) D) E)
E) For the differential equation, find the particular solution y = 0 when x = 0. 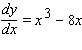A) 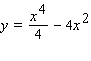B) 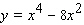C) D) 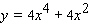E)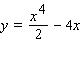

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q52: Decide whether the integral. If the integral

Q53: Nancy s Chocolates estimates that the elasticity

Q54: Find the total value or the given

Q55: Find the total value of the given

Q56: For the given differential equation, find the

Q58: The normal distribution curve, which models the

Q59: Calculate the 5-unit moving average of the

Q60: Find the area of the indicated region.

Q61: Find the total value of the given

Q62: Calculate the 5-unit moving average of the