Solved

Fill in the Blanks So That the Left Side of Each

Question 159

Multiple Choice

Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) B) C) D) E) _____ Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) B) C) D) E) _____ Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) B) C) D) E)


A) Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) B) C) D) E)
B) Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) B) C) D) E)
C) Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) B) C) D) E)
D) Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) B) C) D) E)
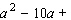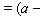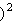
E) Fill in the blanks so that the left side of each is a perfect square trinomial; that is, complete the square. _____ _____ A) 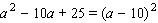B) 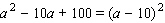C) 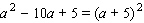D) E)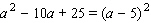

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q154: For the equation, find the coordinates of

Q155: Writing in 1829, former President James Madison

Q156: Solve the equation. Use factoring or the

Q157: Solve the equation using the quadratic formula.

Q158: Use the discriminant to find the number

Q160: Find the vertex and any two convenient

Q161: Solve the equation using the quadratic formula.

Q162: Solve the inequality and graph the solution

Q163: Solve the following equation. Remember, if you

Q164: For the equation, find the coordinates of