Short Answer
Fill in the blanks so that the left side is a perfect square trinomial; that is, complete the square. 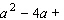 _____
_____ 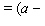 _____
_____ 
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Find an equation that has the given
Q3: Justin wants to fence 3 sides of
Q4: Solve the following quadratic equation by completing
Q5: For the equation, find the coordinates of
Q6: Solve the formula <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8808/.jpg" alt="Solve the
Q8: Use the discriminant to find the number
Q9: Solve the equation. Use factoring or the
Q10: The graph of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8808/.jpg" alt="The graph
Q11: Determine <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8808/.jpg" alt="Determine so
Q12: Solve the equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8808/.jpg" alt="Solve the