Short Answer
Fill in the blanks so that the left side is a perfect square trinomial; that is, complete the square. 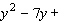 _____
_____ 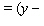 _____
_____ 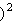
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q22: Solve the inequality and graph the solution
Q23: Solve the following quadratic equation by completing
Q24: Determine <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8808/.jpg" alt="Determine so
Q25: Solve the inequality and graph the solution
Q26: Use the discriminant to find the number
Q28: Use the discriminant to find the number
Q29: Solve the inequality and graph the solution
Q30: Simplify. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8808/.jpg" alt="Simplify. A)
Q31: Multiply both sides of the equation by
Q32: Find an equation that has the given