Multiple Choice
Solve graphically. The sum of two resistances is . Their difference is . Find the two resistances. If we let and be the two resistances, the equations are
A) 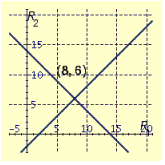
B) 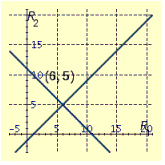
C) 
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q53: Solve, using the substitution method, and
Q54: Draw the graphs of the pair
Q55: Solve, using the substitution method, and
Q56: Draw the graphs of the pair
Q57: Solve the pair of linear equations
Q59: Find the capacity of two trucks if
Q60: Draw the graphs of the pair
Q61: Solve, using the substitution method, and
Q62: How much of a 2% solution and
Q63: Solve, using the substitution method, and