Multiple Choice
Solve graphically. In a concrete mix, there is four times as much gravel as concrete. The total volume is . How much of each is in the mix if
X = the amount of concrete
Y = the amount of gravel
The equations are
A) 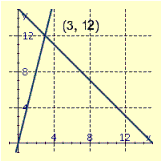
B) 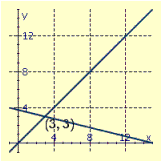
C) 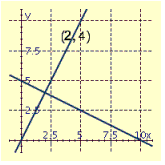
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q29: Solve the pair of linear equations
Q30: Solve, using the substitution method, and
Q31: A sporting goods store carries two types
Q32: A supply duct is to run the
Q33: A farmer has a14%-solution and a 2%-solution
Q35: Draw the graphs of the pair
Q36: A rectangle length is five times as long
Q37: Solve the pair of linear equations
Q38: Solve the pair of linear equations
Q39: Draw the graphs of the pair