Consider the Following Approach to Factoring $$20 x ^ { 2 } + 39 x + 18$$

Multiple Choice

Consider the following approach to factoring. 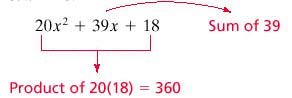$$20 x ^ { 2 } + 39 x + 18$$ We need two integers whose sum is 39 and whose product is 360. To help find these integers, let s prime factor 360. $360 = 5 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 5$ Now by grouping these factors in various ways, we find that $2 \cdot 2 \cdot 2 \cdot 3 = 24,3 \cdot 5 = 15$ and $24 + 15 = 39$ So the numbers are 15 and 24, and we can express the middle term of the given trinomial, $39 x$ , as $15 x + 24 x$ . Therefore, we can complete the factoring as follows: $20 x ^ { 2 } + 39 x + 18 = 20 x ^ { 2 } + 15 x + 24 x + 18 = 5 x ( 4 x + 3 ) + 6 ( 4 x + 3 ) = ( 4 x + 3 ) ( 5 x + 6 )$ Factor the trinomial. $20 y ^ { 2 } + 23 y + 6$

A) (4 y + 3) (8 y + 2)
B) (4 y $-$ 3) (5 y $-$ 2)
C) (4 y + 3) (5 y + 2)
D) (4 y $-$ 3) (5 y + 2)
E) (6 y + 3) (5 y + 3)