Multiple Choice
The graph of  is shown in the figure. As you can see, the graph does not cross the
is shown in the figure. As you can see, the graph does not cross the 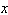 -axis. If the graph did cross the
-axis. If the graph did cross the  -axis, the
-axis, the  -intercepts would be solutions to the equation:
-intercepts would be solutions to the equation: 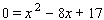 Solve this equation. The solutions will confirm the fact that the graph cannot cross the
Solve this equation. The solutions will confirm the fact that the graph cannot cross the 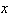 -axis.
-axis. 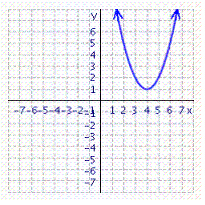
A) 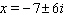
B) 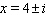
C) 
D) 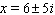
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Solve the equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8671/.jpg" alt="Solve the
Q2: Graph the equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8671/.jpg" alt="Graph the
Q3: Solve the equation by using the quadratic
Q4: Solve the equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8671/.jpg" alt="Solve the
Q5: Solve the equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8671/.jpg" alt="Solve the
Q7: Multiply the complex numbers. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8671/.jpg" alt="Multiply
Q8: Write the radical as a complex number.
Q9: Graph the equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8671/.jpg" alt="Graph the
Q10: Solve the equation by using the quadratic
Q11: Solve the quadratic equation. Use whatever method