Solved

Use the Power-Reducing Formulas to Rewrite the Given Expression in Terms

Question 60

Multiple Choice

Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. A) B) C) D) E) Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. A) B) C) D) E)


A) Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. A) B) C) D) E)
B) Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. A) B) C) D) E)
C) Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. A) B) C) D) E)
D) Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. A) B) C) D) E)
E) Use the power-reducing formulas to rewrite the given expression in terms of the first power of the cosine. A) 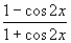B) 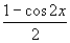C) 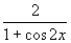D) 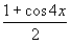E)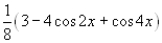

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q55: Multiply; then use fundamental identities to simplify

Q56: Add or subtract as indicated; then use

Q57: Solve the following equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Solve

Q58: Find the exact value of the given

Q59: Find all solutions of the following equation

Q61: Find the exact value of the given

Q62: Which of the following is equivalent to

Q63: Use a double-angle formula to find the

Q64: Solve the multiple-angle equation in the interval

Q65: Which of the following is a solution