The Number of Bacteria in a Culture Is Increasing According

Multiple Choice

The number of bacteria in a culture is increasing according to the law of exponential growth. After 2 hours there are 140 bacteria in the culture and after 4 hours there are 370 bacteria in the culture. Answer the following questions, rounding numerical answers to four decimal places.(i) Find the initial population.(ii) Write an exponential growth model for the bacteria population. Let t represent time in hours.(iii) Use the model to determine the number of bacteria after 8 hours.(iv) After how many hours will the bacteria count be 25,000?

A) (i) 52.9730 ; (ii) 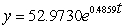; (iii) 2,584.3367 ; (iv) 12.6702 hr
B) (i) 55.1230 ; (ii) 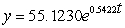; (iii) 5,271.7880 ; (iv) 17.2327 hr
C) (i) 58.7530 ; (ii) 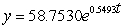; (iii) 8,023.2414 ; (iv) 19.3439 hr
D) (i) 60.3130 ; (ii) 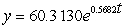; (iii) 10,675.7049 ; (iv) 21.1233 hr
E) (i) 52.9730 ; (ii) 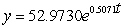; (iii) 3,897.0708 ; (iv) 15.0047 hr