Multiple Choice
The rate of growth 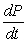 of a population of bacteria is proportional to the square root of t, where P is the population size and t is the time in days
of a population of bacteria is proportional to the square root of t, where P is the population size and t is the time in days 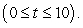 That is,
That is, 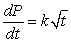 . The initial size of the population is 300. After one day the population has grown to 400. Estimate the population after 9 days. Round your answer to the nearest integer.
. The initial size of the population is 300. After one day the population has grown to 400. Estimate the population after 9 days. Round your answer to the nearest integer.
A)  bacteria
bacteria
B) 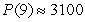 bacteria
bacteria
C) 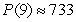 bacteria
bacteria
D) 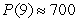 bacteria
bacteria
E) 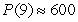 bacteria
bacteria
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Determine the area of the given region.
Q3: Evaluate the following definite integral by the
Q4: The graph of the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg"
Q5: Find the indefinite integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Find
Q6: Find the indefinite integral of the following
Q8: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Evaluate the
Q9: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Solve
Q10: Find the indefinite integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Find
Q11: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Solve
Q12: Find the general solution of the differential