Solved

The Radius, R, of a Circle Is Increasing at a Rate

Question 47

Multiple Choice

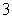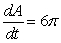The radius, r, of a circle is increasing at a rate of 2 centimeters per minute.Find the rate of change of area, A, when the radius is The radius, r, of a circle is increasing at a rate of 2 centimeters per minute.Find the rate of change of area, A, when the radius is . A) sq cm/min B) sq cm/min C) sq cm/min D) sq cm/min E) sq cm/min .


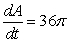A) The radius, r, of a circle is increasing at a rate of 2 centimeters per minute.Find the rate of change of area, A, when the radius is . A) sq cm/min B) sq cm/min C) sq cm/min D) sq cm/min E) sq cm/min sq cm/min
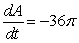B) The radius, r, of a circle is increasing at a rate of 2 centimeters per minute.Find the rate of change of area, A, when the radius is . A) sq cm/min B) sq cm/min C) sq cm/min D) sq cm/min E) sq cm/min sq cm/min
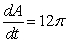C) The radius, r, of a circle is increasing at a rate of 2 centimeters per minute.Find the rate of change of area, A, when the radius is . A) sq cm/min B) sq cm/min C) sq cm/min D) sq cm/min E) sq cm/min sq cm/min
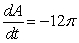D) The radius, r, of a circle is increasing at a rate of 2 centimeters per minute.Find the rate of change of area, A, when the radius is . A) sq cm/min B) sq cm/min C) sq cm/min D) sq cm/min E) sq cm/min sq cm/min
E) The radius, r, of a circle is increasing at a rate of 2 centimeters per minute.Find the rate of change of area, A, when the radius is . A) sq cm/min B) sq cm/min C) sq cm/min D) sq cm/min E) sq cm/min sq cm/min

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q42: A ball is thrown straight down from

Q43: A man 6 feet tall walks at

Q44: Find d<sup>2</sup>y/dx<sup>2</sup> in terms of x and

Q45: Find the derivative of the function <img

Q46: Suppose the position function for a free-falling

Q48: Find the derivative of the function <img

Q49: Use the alternative form of the derivative

Q50: Assume that x and y are both

Q51: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Evaluate for

Q52: Find the slope m of the line