Multiple Choice
A 25-foot ladder is leaning against a house (see figure) . If the base of the ladder is pulled away from the house at a rate of 2 feet per second, the top will move down the wall at a rate of 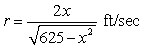 where x is the distance between the base of the ladder and the house. Find the rate r when x is 20 feet.
where x is the distance between the base of the ladder and the house. Find the rate r when x is 20 feet. 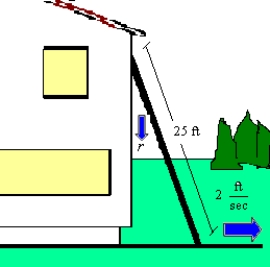
A) 
B) 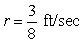
C) 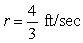
D) 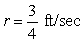
E) 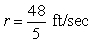
Correct Answer:

Verified
Correct Answer:
Verified
Q6: Suppose that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Suppose that
Q7: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Let .Determine
Q8: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Find the
Q9: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Find the
Q10: Find the limit (if it exists): <img
Q12: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8702/.jpg" alt="Let and
Q13: Determine the following limit. (Hint: Use the
Q14: Find the limit (if it exists). Note
Q15: Find the limit (if it exists). <img
Q16: Find the x-values (if any) at which