Describe the Right-Hand and the Left-Hand Behavior of the Graph

Multiple Choice

Describe the right-hand and the left-hand behavior of the graph of .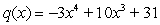

A) Because the degree is even and the leading coefficient is negative, the graph falls to the left and falls to the right.
B) Because the degree is even and the leading coefficient is negative, the graph rises to the left and falls to the right.
C) Because the degree is even and the leading coefficient is negative, the graph falls to the left and rises to the right.
D) Because the degree is even and the leading coefficient is negative, the graph rises to the left and rises to the right.
E) Because the degree is odd and the leading coefficient is negative, the graph rises to the left and rises to the right.