Solved

Express in the Standard Form of a Quadratic Function

Question 99

Multiple Choice

Express 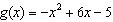Express in the standard form of a quadratic function. A) B) C) D) E) in the standard form of a quadratic function.


A) Express in the standard form of a quadratic function. A) B) C) D) E)
B) Express in the standard form of a quadratic function. A) B) C) D) E)
C) Express in the standard form of a quadratic function. A) B) C) D) E)
D) Express in the standard form of a quadratic function. A) B) C) D) E)
E) Express in the standard form of a quadratic function. A) 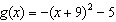B) 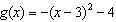C) 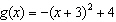D) 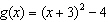E)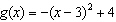

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q94: Write an expression that represents the length

Q95: Find the product and simplify. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8673/.jpg"

Q96: Using the graph below find the x

Q97: A diver jumps off the springboard and

Q98: Is the polynomial linear or nonlinear? <img

Q100: When you add two polynomials the result

Q101: When you add two polynomials the result

Q102: Divide the expressions. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8673/.jpg" alt="Divide the

Q103: When you divide two polynomials each of

Q104: Divide the expressions. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8673/.jpg" alt="Divide the