Solved

If and Are Matrices Then When

Question 168

Multiple Choice

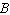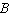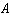If If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. and If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. are matrices then If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. when...


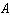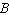A) If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. is the inverse matrix of If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. .
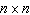B) If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. is an identity matrix.
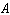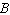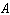C) If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. and If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. are If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. matrices.
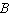D) If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. and If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. are identical matrices.
E) If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. and If and are matrices then when... A) is the inverse matrix of . B) is an identity matrix. C) and are matrices. D) and are identical matrices. E) and have the same dimension. have the same dimension.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q163: Solve the equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8673/.jpg" alt="Solve the

Q164: The box below lists the nutritional information

Q165: The following is the nutritional information for

Q166: Which one of the following is the

Q167: Perform the matrix operation as indicated. <img

Q169: To divide rational expressions multiply by the

Q170: If Sue is able to clean the

Q171: Which one of the following is the

Q172: Simplify the complex fraction. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8673/.jpg" alt="Simplify

Q173: Any number that makes the _ of