Solved

A Penny Is Dropped from a High-Rise Building That Is

Question 5

Multiple Choice

A penny is dropped from a high-rise building that is 350 feet high. After 8.4 seconds, the penny hits the ground. Which one of the following quadratic models describe the height of the penny above ground as a function of the time elapsed since the penny was dropped?


A) A penny is dropped from a high-rise building that is 350 feet high. After 8.4 seconds, the penny hits the ground. Which one of the following quadratic models describe the height of the penny above ground as a function of the time elapsed since the penny was dropped? A) B) C) D) E)
B) A penny is dropped from a high-rise building that is 350 feet high. After 8.4 seconds, the penny hits the ground. Which one of the following quadratic models describe the height of the penny above ground as a function of the time elapsed since the penny was dropped? A) B) C) D) E)
C) A penny is dropped from a high-rise building that is 350 feet high. After 8.4 seconds, the penny hits the ground. Which one of the following quadratic models describe the height of the penny above ground as a function of the time elapsed since the penny was dropped? A) B) C) D) E)
D) A penny is dropped from a high-rise building that is 350 feet high. After 8.4 seconds, the penny hits the ground. Which one of the following quadratic models describe the height of the penny above ground as a function of the time elapsed since the penny was dropped? A) B) C) D) E)
E) A penny is dropped from a high-rise building that is 350 feet high. After 8.4 seconds, the penny hits the ground. Which one of the following quadratic models describe the height of the penny above ground as a function of the time elapsed since the penny was dropped? A) 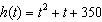B) 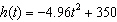C) D) 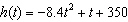E)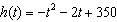

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Find the maximum or minimum value of

Q2: Find a quadratic function g whose graph

Q3: The quadratic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8728/.jpg" alt="The quadratic

Q4: A diver jumps off the springboard and

Q6: The graph of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8728/.jpg" alt="The graph

Q8: Which one of the following graphs illustrate

Q9: Find the discriminant of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8728/.jpg" alt="Find

Q10: Solve the equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBX8728/.jpg" alt="Solve the

Q11: Using the graph below, find the y

Q87: A rectangular parking lot is 22 feet