Multiple Choice
Solve the inequality and graph the solution on the real number line.
A) Solution: 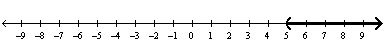
B) Solution: 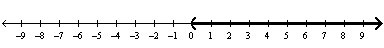
C) Solution: 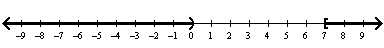
D) Solution: 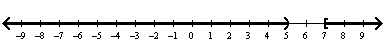
E) Solution: 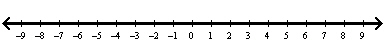
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q23: Determine the intervals for which
Q24: Determine the intervals for which
Q25: Find the critical numbers. <span
Q26: The height h (in feet)of an
Q27: Use a graphing calculator to solve
Q29: Graph the solution to the inequality
Q30: Find the intercepts of
Q31: What term should be added to
Q32: Solve the equation by using the
Q33: Solve the equation by completing the