Solved

Let V Be the Set of All Vectors

Question 9

Short Answer

Let V be the set of all vectors Let V be the set of all vectors 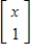, where x is in R. Using the usual rules for vector addition and scalar multiplication in R<sup>2</sup>, determine if V is a vector space, and if not explain why. , where x is in R. Using the usual rules for vector addition and scalar multiplication in R2, determine if V is a vector space, and if not explain why.

Correct Answer:

verifed

Verified

V is not a vector sp...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q4: Determine the dimension of the subspace S

Q5: Determine if the set of vectors <img

Q6: The set V of all nonnegative real

Q7: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="If then

Q8: Determine the dimension of the subspace S

Q10: Determine if the given set is a

Q11: In the vector space <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="In

Q12: Determine if <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Determine if

Q13: In the vector space <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="In

Q14: If V is a vector space and