Solved

In the Vector Space , Let S Be the Set

Question 36

Short Answer

In the vector space In the vector space , let S be the set of all sequences such that there exists some such that for all (all eventually-zero sequences). Determine if S is a subspace of , and if not explain why. , let S be the set of all sequences In the vector space , let S be the set of all sequences such that there exists some such that for all (all eventually-zero sequences). Determine if S is a subspace of , and if not explain why. such that there exists some In the vector space , let S be the set of all sequences such that there exists some such that for all (all eventually-zero sequences). Determine if S is a subspace of , and if not explain why. such that In the vector space , let S be the set of all sequences such that there exists some such that for all (all eventually-zero sequences). Determine if S is a subspace of , and if not explain why. for all In the vector space , let S be the set of all sequences such that there exists some such that for all (all eventually-zero sequences). Determine if S is a subspace of , and if not explain why. (all eventually-zero sequences). Determine if S is a subspace of In the vector space 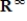, let S be the set of all sequences 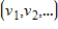such that there exists some 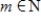such that 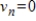for all 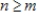(all eventually-zero sequences). Determine if S is a subspace of , and if not explain why. , and if not explain why.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q31: Determine if <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Determine if

Q32: Every vector space V has a finite

Q33: Determine the dimension of the subspace S

Q34: Determine if the set <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Determine

Q35: Find a basis for the subspace S

Q37: Determine if the set of vectors <img

Q38: Determine the dimension of the subspace S

Q39: Find a basis for the subspace S

Q40: Determine if the set of vectors <img

Q41: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="If and