Solved

If and , Where , and

Question 50

True/False

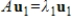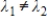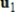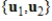If If and , where , and and are nonzero vectors, then is linearly independent. and If and , where , and and are nonzero vectors, then is linearly independent. , where If and , where , and and are nonzero vectors, then is linearly independent. , and If and , where , and and are nonzero vectors, then is linearly independent. and If and , where , and and are nonzero vectors, then is linearly independent. are nonzero vectors, then If and , where , and and are nonzero vectors, then is linearly independent. is linearly independent.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q45: Use the Power Method with scaling to

Q46: The coefficient matrix for a system of

Q47: Determine the rotation and dilation that result

Q48: Diagonalize the matrix A, if possible.<br> <img

Q49: Determine which of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Determine which

Q51: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Compute if

Q52: Find the characteristic polynomial, the eigenvalues, and

Q53: Factor the matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Factor the

Q54: If A and <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="If A

Q55: The coefficient matrix for a system of