Solved

If B1, B2 Are Bases for a Given Subspace, and a Is

Question 41

True/False

If B1, B2 are bases for a given subspace, and A is the change of basis matrix from B1 to B2, then A is invertible, and
If B<sub>1</sub>, B<sub>2</sub> are bases for a given subspace, and A is the change of basis matrix from B<sub>1</sub> to B<sub>2</sub>, then A is invertible, and 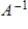is the change of basis matrix from B<sub>2</sub> to B<sub>1</sub>. is the change of basis matrix from B2 to B1.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q36: Find the change of basis matrix from

Q37: The null space of an <br> <img

Q38: Convert the coordinate vector <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg"

Q39: Find <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Find

Q40: Determine the null space of<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg"

Q42: Find the change of basis matrix from

Q43: Find the change of basis matrix from

Q44: If B<sub>1</sub>, B<sub>2</sub>, and B<sub>3</sub> are all

Q45: Let <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Let

Q46: Find all values of <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg"