Solved

If Is a Linear Dependent Set of Nonzero Vectors

Question 11

True/False

If
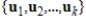If is a linear dependent set of nonzero vectors in a vector space V, and is any inner product on V, then there exists such that . is a linear dependent set of nonzero vectors in a vector space V, and
If is a linear dependent set of nonzero vectors in a vector space V, and is any inner product on V, then there exists such that . is any inner product on V, then there exists
If is a linear dependent set of nonzero vectors in a vector space V, and is any inner product on V, then there exists such that . such that
If is a linear dependent set of nonzero vectors in a vector space V, and is any inner product on V, then there exists 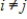such that .
.

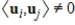
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q6: Find the weighted least squares line for

Q7: Determine the values of a (if any)

Q8: Determine all values of a such that

Q9: Use the Gram-Schmidt process to convert the

Q10: Find the Fourier approximation <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg"

Q12: Evaluate <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBMC1039/.jpg" alt="Evaluate

Q13: The following is an inner product on

Q14: Use the Gram-Schmidt process to convert the

Q15: Find the weighted least squares line for

Q16: Find the Fourier coefficients for the function