Consider the Following Payoff Matrix for a 2-Player Game Where

Not Answered

Consider the following payoff matrix for a 2-player game where the payoffs have the usual connotation. The first number in each cell represents the payoff to Player #1 and the second number the payoff to Player #2.
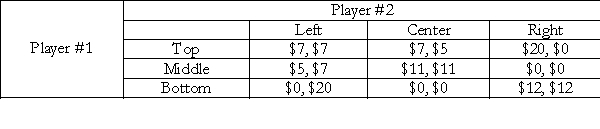(a) What is/are the Nash equilibrium/equilibria of this game? (b) Explain your answer very briefly. (c) Suppose the two players have each bought a ticket worth $8 to play this game. Both players know that the other player has paid $8.00 to play the game. How do you think the payment of this fee may change the equilibrium outcome of the game from one where no such fee is paid?